SPICILE
UNE MANIFESTATION INATTENDUE
Le jeu à pile ou face.
Si je joue 100 parties de 1000 coups et si je joue 1000 parties de 100 coups, dans les deux cas, j’aurais joué 100000 coups.
Mais, dans 100 parties de 1000 coups, j’ai 100 retours à zéro (à chaque début de nouvelle partie). Dans 1000 parties de 100 coups, j’ai 1000 retours à zéro.
L’équipartition, (autant de pile que de face en cours de partie), n’est pas la même dans les parties de 100 coups que dans les parties de 1000 coups.
Dans une partie de 100 coups, l’équipartition est de 6,02 mais, dans une partie de 1000 coups l’équipartition n’est que de 24,25. (Si la progression était géométrique, l’équipartition serait de : 6,02 x 10 = 60,2 puisque 1000 coups est = 100 x10).
La discrépance, (en quelque sorte l’inverse de l’équipartition), n’est pas la même, bien évidemment, dans les parties de 100 coups que dans les parties de 1000 coups.
Et, si nous jouons simultanément, à plusieurs parties panachées, de 100 coups et de 1000 coups, nous obtenons des résultats émergents, lisibles sur une sinusoïde (à partir du paradoxe de Parrondo repris et prolongé par Amengual puis l’Obédience.).
Nota : il semblerait que « l’information » qui gère l’équipartition et la discrépance, « se mélange les crayons ». Mais les résultats sont fidèles, cycliques. Pour faire simple, des parties de 1000 coups, profitent d’une bien meilleure équipartition, calculable. Le minimum de : 24,25 représente le bas de la sinusoïde et le maximum de 60,2 représente le haut de la sinusoïde. Les parties de 1000 coups, oscillent donc avec une équipartition comprise entre : 24,25 et 60,2. (Pour simplifier autant que faire se peut).
Une vie politique ou plus simplement, un mandat, peut être, dans certains cas, assimilé à plusieurs parties jouées simultanément dans l’équivalent d’un espace fermé, tel que, une partie de plusieurs parties, (dont l’une est essentielle, par exemple la présidentielle). Parfois, les actions à court terme, moyen terme et long terme (sorte d’équivalence des parties à 100 coups et 1000 coups), se superposent simultanément. Le kairos correspond à la partie à 60,2 d’équipartition, le haut de la sinusoïde.
La définition de Boll ne peut plus alors être appliquée.
Rappel :
Boll : « le nombre des retours à l’équipartition, augmente comme la racine carrée du nombre de coups. La proportion de ces retours varie comme l’inverse de la racine carrée du nombre des coups ».
Suarès : « le désordre est bien puissant quand il s’organise ».
Bazile : « l’avantage du désordre, c’est qu’il se transforme en ordre, tôt ou tard ».
Confucius : « celui qui aime à apprendre est bien prés du savoir »
Sur la rareté de l'équipartition
N. Lygeros
La lecture de différents articles et études scientifiques dans un cadre non mathématique nous a permis de constater que la moindre différence de proportions est considérée comme révélatrice d'un phénomène scientifique. Le substrat mathématique de cette méthodologie est essentiellement constitué par ce que nous nommons la loi des grands nombres. Cependant celle-ci est interprétée de manière extrême et voire caricaturale. En effet la loi des grands nombres affirme que des évènements indépendants générés par la même procédure ont le même ordre de grandeur. Néanmoins hors du strict cadre mathématique, le même ordre de grandeur est remplacé par l'égalité. Ainsi la moindre différence est sensée avoir un sens. Afin d'expliciter l'erreur fondamentale de cette approche nous allons examiner un cas strictement mathématique dépourvu de tout autre contexte. Si nous lançons 2m fois une pièce normale, notons a(m) la probabilité d'obtenir m fois Pile et m fois Face. C'est ce que nous nommons l'équipartition. Le calcul de cette probabilité est relativement trivial en combinatoire puisqu'il correspond au coefficient central, le plus élevé, de la ligne numéro 2m du triangle de Pascal, divisé par la somme totale des coefficients de cette ligne. Or le coefficient central, c'est le nombre de combinaisons de 2m objets pris m à m, sans répétition i.e. C(m,2m) et la somme totale correspond au nombre de parties d'un ensemble à 2m éléments i.e. 2^(2m). Ainsi a(m)=C(m,2m)/2^(2m) et il est facile de montrer que cette valeur tend vers zéro en l'infini. Plus explicitement en développant C(m,2m) en factorielles et en appliquant la formule de Stirling à savoir n! ~ (n/e)^n*sqrt(2*Pi*n) nous obtenons : ((2m)!/(m!*m!))/2^(2m) ~ (2m/e)^(2m)*sqrt(2*Pi*2m)/ (2^(2m)*(m/e)^m*sqrt(2*Pi*m)*(m/e)^m*sqrt(2*Pi*m)) ~ 1/sqrt(Pi*m).
Par exemple, si nous lançons 10.000 fois une pièce de monnaie, l'équipartition a une probabilité équivalente à 1/(100*sqrt(Pi)) et donc inférieure à 1 %. Aussi des résultats qui sont en dehors de cette zone, ne peuvent être considérés comme révélateurs d'un phénomène quelconque. Toute l'information de la non équipartition est contenue dans le code mathématique et n'a aucun sens en dehors de celui-ci, aussi toute autre interprétation ne peut être qu'erronée et ce quelque soit le domaine. Par ailleurs lorsque l'échantillonnage est très faible, de l'ordre d'une dizaine de cas, même s'il y a une équiprobabilité théorique, une légère différence dans les pourcentages est plus probable que l'équipartition. Pour 10 cas par exemple, il est deux fois plus probable d'obtenir 6 et 4 que 5 et 5 puisque la partition avec 5 est unique alors qu'avec 6 elle est double. A nouveau donc, cette différence n'est pas révélatrice d'un phénomène autre que purement mathématique. De manière générale, l'utilisation de la mentalité mathématique doit être effectuée avec précaution car la moindre erreur d'interprétation dans un cadre scientifique conduit à des conclusions essentiellement fausses. L'outil mathématique sans l'esprit mathématique ne représente pas un avantage scientifique mais bien souvent une erreur cognitive caractérisée. |
-3-L’équipartition
On a déjà parlé d’équiparition en fin de partie, qui correspond au “coup nul”. On a vu que le “coup nul” n’est possible que si le nombre des coups est pair.
Pour illustrer cette idée joignons le tableau ci-contre, qui montre au premier coup d’oeil que la compensation exacte devient de plus en plus rare, au fur et à mesure que les parties s’alongent.
Par exemple: si Patrice et Fabien jouent 1000 parties de 100 coups, sur ces 1000 parties, il y en aura environ 80 qui se termineront par un coup nul. Si au contraire, ils jouent 100 parties de 1000 coups, sur ces 100 parties, il y en aura entre 2 et 3 qui se termineront par un coup nul.
Le tableau et le graphique ci-contre sont ignorés de la plupart des joueurs, qui croient “dur comme fer” à la nécessité d’une rigoureuse compensation “à la longue”: cette erreur incontestable sert de base à la plupart des systèmes.
3-4-La ruine inévitable des joueurs
Tout d’abord il faut savoir qu’un jeu où n’intervient pas l’habilité des joueurs est dit équitable pour un joueur si l’espérance mathématique qu’il en attend est nulle. Dans ce cas, la moyenne arithmétique de ses gains, s’il joue indéfiniment au même jeu, tendra à se rapprocher de zéro. Le jeu sera dit avantageux si cette espérance est positive, désavantageux si elle est négative.
Ainsi dans un jeu équitable, la ruine est certaine pour le joueur invétéré qui joue indéfiniment contre tous les adversaires qu’il rencontre, car si la moyenne des gains tend à se rapprocher de zéro, le gain total oscille en général entre des valeurs positives et négatives de plus en plus grandes, jusqu’à ce qu’il atteingne la valeur qu’avait la fortune du joueur au début du jeu changée de signe. De même si deux joueurs jouent indéfiniment l’un contre l’autre, l’un des deux finira par être ruiné. Dans le cas où les deux joueurs ont le même rôle dans le jeu, ce sera le plus pauvre qui aura le plus de chances d’être ruiné le premier, mais cela n’a rien de certain.
A un jeu désavantageux, la ruine est a fortiori certaine. Cependant un jeu désavantageux peut être raisonnable, si on n’y joue pas trop longtemps, comme la roulette; par contre un jeu peut être équitable ou même avantageux et pourtant insensé comme le montre le “paradoxe de Saint-Pétersbourg”, ou plus simplement le jeu où l’on aurait 9999 chances sur 10000 de perdre la totalité de sa fortune et 1 chance sur 10000 de la voir multipliée par 9999.
On a déjà parlé d’équiparition en fin de partie, qui correspond au “coup nul”. On a vu que le “coup nul” n’est possible que si le nombre des coups est pair.
Pour illustrer cette idée joignons le tableau ci-contre, qui montre au premier coup d’oeil que la compensation exacte devient de plus en plus rare, au fur et à mesure que les parties s’alongent.
Par exemple: si Patrice et Fabien jouent 1000 parties de 100 coups, sur ces 1000 parties, il y en aura environ 80 qui se termineront par un coup nul. Si au contraire, ils jouent 100 parties de 1000 coups, sur ces 100 parties, il y en aura entre 2 et 3 qui se termineront par un coup nul.
Le tableau et le graphique ci-contre sont ignorés de la plupart des joueurs, qui croient “dur comme fer” à la nécessité d’une rigoureuse compensation “à la longue”: cette erreur incontestable sert de base à la plupart des systèmes.
3-4-La ruine inévitable des joueurs
Tout d’abord il faut savoir qu’un jeu où n’intervient pas l’habilité des joueurs est dit équitable pour un joueur si l’espérance mathématique qu’il en attend est nulle. Dans ce cas, la moyenne arithmétique de ses gains, s’il joue indéfiniment au même jeu, tendra à se rapprocher de zéro. Le jeu sera dit avantageux si cette espérance est positive, désavantageux si elle est négative.
Ainsi dans un jeu équitable, la ruine est certaine pour le joueur invétéré qui joue indéfiniment contre tous les adversaires qu’il rencontre, car si la moyenne des gains tend à se rapprocher de zéro, le gain total oscille en général entre des valeurs positives et négatives de plus en plus grandes, jusqu’à ce qu’il atteingne la valeur qu’avait la fortune du joueur au début du jeu changée de signe. De même si deux joueurs jouent indéfiniment l’un contre l’autre, l’un des deux finira par être ruiné. Dans le cas où les deux joueurs ont le même rôle dans le jeu, ce sera le plus pauvre qui aura le plus de chances d’être ruiné le premier, mais cela n’a rien de certain.
A un jeu désavantageux, la ruine est a fortiori certaine. Cependant un jeu désavantageux peut être raisonnable, si on n’y joue pas trop longtemps, comme la roulette; par contre un jeu peut être équitable ou même avantageux et pourtant insensé comme le montre le “paradoxe de Saint-Pétersbourg”, ou plus simplement le jeu où l’on aurait 9999 chances sur 10000 de perdre la totalité de sa fortune et 1 chance sur 10000 de la voir multipliée par 9999.
L'application Calcul Des Probabilités JeuSea principes se retrouvent dans lea jeux de casinos légèrement altérés pour lea chances simples, de la boule et de la roulette, du trente-et-quarante, de l'écarté ou du baccara on de certains jeux casino chinois. Dana les cas plus compliqué des 'chances multiples de Ia boule et de la roulette, du quatre-quatre ou du craps, ou encore de la répartition des cartes au baccara et à l'écarté, le calcul des ,probabilités intervient aussi. Le jeu de pile ou face est par définition équitable puisque la probabilité de sortir, pour pile comme 'pour face, est de 1 coup sur deux, soit 1/2. Cette probabilité demeure, pie1 pie soit l'ordre du coup, quel pie soit le nombre de coups dans une partie. Léa jeux de casinos ne sont pas tout ii fait équitables, mais lea problèmes peuvent s'y traiter de façon idéntipie, pie il s'agisse de ccliii du retour à i'équilibre ou de l'espérance mathématique. La croyance est très répandue pie au bout d'un certain ñombre de parties lea deux éventualités .(pile ou face, pair ou impair, rouge ou noir) doivent sortir un nombre égal de fois. C'est cc pion appelle l'équipartition ou plus communément l'équilibre. | Ecart Et Equipartition Un instant de réflexion fait apparaître pie si cette loi était exacte il n'y aurait jamais d'écart : ne peut-on considérer chaque coup comme théoriquement la fin d'une longue partie? Le calcul confirme la logiciel. L'équipartition n'est pie un cas particulier de l'écart. L'équipartition c'est, en somme, l'écart nul. Sous cet angle, on peut des bra observer pie dans la masse des éventualités des écarts, qui s'accroche avec be nombre des parties, l'équarri tit ion devient un phénomène particulier dont lea chances diminuent. Si, sur deux coups, l'équipartition présente une probabilité de 0,5, an bout de quatre coups, cette probabilité n'est plus que de 0,375. La probabilité de l'écart passe, à l'inverse de 0,5, à 0,625. Au fur et à mesure que s'accroît le nombre de parties la distorsion des probabilités augmente. Au bout de 10 coups, lea bouts probabilités sont 0,25 pour l'équipartition, 0,75 pour l'écart; au bout de 20 coups, 0,176 pour l'équipartition, 0,824 pour l'écart; au bout de 40 coups, 0,126 pour l'équipartition, 0,874 pour l'écart. Au bout de 1 000 coups lea probabilités tombent pour l'équipartition à 0,025 alors qu'elles passent à 0,975 pour l'écart. En poussant de plus en plus on volt pie l'on franchit le seuil of pratiquement l'équipartition devient impossible; l'écart devient donc la règle. Pascal, ndtamment, s'efforce de calculer lea pro. babi lités de chacun des coups possibles, d'une part de l'équipartition, d'autre part des écarts ; il mit au point le triangle arithmétique (tabl. II) qul donne la probabilité des sorties. Ce triangle se construit de la façon suivante : on macnt sur Ia première ligue lea ehiifres suivants 0110 sun la seconde ligne on macnt les chiffres doués par l'addition du chiffre au-dessus et du chiffre Immédiatement à gauche et l'ou à 01210 même opération pour la troisième ligue: 013310 si l'on additionne ligne par ligne les chiffres dans le sons horizontal nous avons le nombre de sorties possibles. À la première ligne (c'est le premier coup) nous avons bien deux solutions possible : 1 rouge (ou pile), 1 noir (ou face). Ce que l'on écrit: I fois pile, 1 fois face. À la troisième partie nous avons $ solutions différentes: 1 fois = 0 pile, 3 face 3 fois = pile, 2 face 3 fois = 2 pile, 1 face 1 fois = 3 pile, 0 face | |||||||
7. Conclure sur la r´ecurrence de la chaˆıne.
1. Quand la dimension augmente, le nombre de chemins augmente et les chances de revenir au
point de d´epart s’amenuisent. Une trajectoire peut avoir son projet´e qui retourne au point
initial sans elle mˆeme le faire. La propri´et´e de r´ecurrence de la chaˆıne peut donc ˆetre perdue
en augmentant la dimension.
Demander à votre entourage de choisir au hasard un nombre entre 1 et 9. Pensez-vous que les réponses seraient uniformes, avec autant de 1 que de 2, de 3… ? Eh bien non. Presque un tiers choisira le 7 et 3 % seulement le 1, rappelait le mathématicien et professeur au Laboratoire d’informatique fondamentale de Lille (université de Lille) Jean-Paul Delahaye, dans un article de Pour la science en mars 2006. « On a longtemps cru que c'était parce que 7 n’avait pas de propriétés mathématiques particulières, mais d'autres expériences ont montré que ce n'était valable qu’en Europe ou aux Etats-Unis. D’autres pays “préfèrent” le 2, le 3… C'est donc un biais culturel », explique Nicolas Gauvrit, enseignant-chercheur à l’Ecole pratique des hautes études au laboratoire Cognitions humaine et artificielle (CHArt).
Ce dernier, avec Jean-Paul Delahaye, a voulu savoir si le cerveau était un bon générateur de nombres aléatoires ou pas, comme ils l'expliquent dans Behavior Research Methods en décembre 2013. Ainsi, 68 enfants de 7 à 11 ans ont été invités à imaginer tirer huit fois à pile ou face (en réalité avec un jeton tombant sur le vert ou le rouge). La conclusion est que le cerveau est biaisé et qu'il a tendance à éviter les séries simples, comprenant par exemple l’alternance rouge-vert.
Ce constat est renforcé par un travail non encore publié de la même équipe. 34 adultes de 20 à 55 ans ont produit des suites de 10 symboles parmi A, B, C et D. Ces participants ont là aussi été plus complexes que le simple hasard, évitant les successions simples de lettres.
« Le décalage qu'on observe entre le “vrai” hasard, où chaque tirage est équiprobable, et les productions humaines – plus complexes, c’est-à-dire exemptes de cycles, répétitions... – conforte l'idée que l'homme raisonne fondamentalement de manière probabiliste, conformément au paradigme...« La chance ne sourit qu’aux esprits bien préparés. » Cette phrase est de Louis Pasteur (1822-1895), qui découvrit notamment les principes de la « pasteurisation » ou encore le vaccin contre la rage. Pasteur avait l’esprit préparé, et a trouvé ce qu’il cherchait. Certaines de ses découvertes ont-elles été guidées par la sérendipité, l’art de trouver ce que l’on ne cherche pas ?
--A noter que quelques applications de ce phénomène peuvent apporter des réponses sur la façon imaginative de gérer des jeux lucratifs tel que la Roulette des casinos...En effet, si nous perdons tout le temps en essayant de faire des prédictions,...que faisons nous en comparant les sélections inverses de notre cerveau ?Non, le cerveau n'est pas capable de générer de l'aléatoire pour la simple raison qu'il ne sait que se baser sur des choses connues.
Il ne sait même pas reconnaître l'aléatoire : si on présente à plusieurs personnes des motifs différents censés représenter un tirage aléatoire de quelques milliers de points, la plupart désigneront comme aléatoire celui qui est "quasi uniformément réparti" alors qu'en théorie, ca n'arrive jamais.
le cerveau est il capable de générer de l'aléatoire?
la réponse est oui: dans la vie courante un individu même d'un tempérament très posé peut brusquement prendre une décision d'ordre professionnel ou privé absolument imprévisible et que lui-même ne comprendra pas plus tard si jamais cette décision s'avère calamiteuse pour lui même ou pour les autres. On peut citer des exemples historiques à ce propos de personnages importants ou moins importants qui ont surpris tout le monde y compris eux mêmes par des idées farfelues suivies de décisions tout autant inconséquentes: Néron dans l'Antiquité romaine était de cette race là, mais aussi plus récemment le général français Gamelin en 1939 au début de la seconde guerre mondiale. Et dans les entreprises et les administrations parfois on voit des choses franchement surprenantes! de même sur la route on voit aussi des comportements très aléatoires chez certains automobilistes...
L'esprit humain explore et analyse instantanément tout ce qui passe à sa portée. Rien n'est, pour lui, indifférent ou banal : il classe, trie, organise, hiérarchise. Cette efficacité dans la recherche de régularités ne cesse de surprendre les chercheurs en sciences cognitives qui découvrent les capacités de nos algorithmes internes. Ceux-ci nous permettent, par exemple, de repérer des corrélations complexes dans une figure (voir la figure 1).
Ce travail du cerveau, effectué sans relâche et sans que nous en ayons conscience sur toutes les informations que reçoivent et élaborent nos sens – lesquels ne sont jamais de simples récepteurs –, a quelques contreparties défavorables. L'une d'elle est l'étonnante infirmité que nous présentons tous face aux tâches de production d'aléas.
Nous avons évoqué dans l'article de décembre 2004 l'irrépressible biais d'alternances – quand nous tentons de produire une suite aléatoire de pile ou face, nous exagérons la proportion d'alternance pf ou fp par rapport aux répétitions pp ou ff – et l'étrange biais de positivité – si on demande à 100 personnes de choisir au hasard un des deux mots oui ou non, plus de 60 pour cent choisissent oui.
Nicolas Gauvrit est maître de conférences en mathématiques à l'université d'Artois et psychologue du développement. Il est l'auteur du blog Raison et psychologie (www.scilogs.fr/raisonetpsychologie/). Il est aussi chercheur en sciences cognitives au Laboratoire CHArt de l'école pratique des hautes études à Paris.
Nous allons aujourd'hui constater, sur quelques situations géométriques, que, pour un humain, jamais rien n'est vraiment au hasard. Certains des résultats mentionnés ont été découverts dans le cadre d'activités de recherche financées par les militaires canadiens. Ceux-ci pensent que la connaissance des biais logiques et géométriques de fonctionnement de notre esprit, lorsque nous poursuivons un fugitif, améliorerait l'efficacité de nos stratégies de traque.
Nous avons tendance à surestimer ou sous-estimer la probabilité qu'un événement (dramatique ou anecdotique) survienne dans notre existence. Or, tout ce qui nous arrive survient par hasard, c’est la science qui le dit.
Les sciences ont prouvé que notre cerveau ne savait pas comment se comporter avec le hasard, car nous ne savions pas «gérer» le fait de ne pas réussir à «prévoir» ce qui va se produire. Déstabilisés, nous cherchons donc, pour nous rassurer, à émettre des intuitions que nous transformons en pronostics. Dans certains cas, nous surestimons la probabilité que quelque chose arrive. Dans d’autres, au contraire, nous sous-estimons cette probabilité.
Suivant le même principe de sous-estimation des probabilités, l’esprit humain a une tendance assez étrange à s’imaginer que les événements dramatiques ne peuvent pas tous survenir en même temps, «comme si le hasard les répartissait de manière uniforme sur l’année», ironise Nicolas Gauvrit. Cette tendance erronée est appelée la «loi des séries». Elle éveille parfois les soupçons de «malédiction», comme lorsque plusieurs accidents meurtriers de train (en juillet 2013) ou d’avion (en 2014) se succèdent. Parfois même, le hasard mathématique sert d’engrais pour alimenter les théories du complot qui fleurissent sur les réseaux sociaux et les forums.
«La probabilité que trois avions tombent cette semaine est infime. Mais si l'on pose la question: “Quelle est la probabilité que trois avions s'écrasent la même semaine au cours des dix dernières années écoulées?”, la probabilité monte à 60%.»
«En résumé, insiste Nicolas Gauvrit, il faut juste faire comprendre à votre cerveau que “le hasard” n’est pas synonyme de régularité. Nous sommes globalement incapables de produire du hasard. Aujourd’hui, aucun homme sur terre ni aucun programme informatique au monde ne sait créer du “pur hasard”.»
Le biais d’alternance est intuitivement convoqué dans les jeux où les options offertes aux acteurs sont binaires. Au jeu du lancer de pièce, nous avons tous tendance à croire qu’un «pile» va succéder à un «face» dans 60% des cas, alors que la probabilité reste de 50% à chaque nouveau lancé. Par ailleurs, plus le tirage est uniforme, plus nous exagérons la probabilité qui va suivre. Après une série de trois «pile», nous imaginons dans 80% des cas que notre lancer aboutira à un «face», alors que la probabilité est encore et toujours de 50%.
Publié 14.04.2017 par Nicolas Gauvrit
On atteint à 25 ans un pic de
performances cognitives, à la fois en termes de vitesse et de complexité
Les neurologues utilisent parfois une tâche étonnamment simple pour
détecter des traumatismes du lobe frontal : ils vous demandent de créer
une suite de chiffres qui soient le plus aléatoire possible. On appelle
cela une tâche de production aléatoire d'items. En cas de traumatisme
frontal (à l'avant du cerveau, donc), vous risquez de donner des
réponses trop stéréotypées, trop régulières--------------------------------------------------------------------------
vous risquez de donner des réponses trop stéréotypées, trop régulières, tel que 123412123. Au contraire, si tout va bien, vous serez capables de former une suite raisonnablement aléatoire — c'est-à-dire complexe. Pourquoi ? parce que produire un hasard de qualité suppose des compétences cognitives de haut niveau (attention, inhibition, mémoire à court terme) pour lesquelles le lobe frontal est essentiel.
La meilleure définition mathématique du hasard repose sur l'idée de complexité. Plus précisément, une suite est aléatoire si elle a une grande complexité algorithmique, qui est définie comme la taille du plus court programme permettant de la créer.
Grâce au travail initié par Hector Zenil et Jean-Paul Delahaye notamment, nous avons pourtant pu créer une méthode efficace pour estimer de manière fiable la complexité de n'importe quelle suite.
Cette méthode, nous venons de l'appliquer à l'étude du développement cognitif au cours de la vie entière dans une étude publiée cette semaine. Lorsque nous essayons de produire une suite aléatoire, celle-ci sera d'autant plus complexe que nos capacités cognitives sont aiguisées. Ainsi, en étudiant la complexité des suites produites par des personnes qui essaient de fournir des réponses imprévisibles ou sans structure, nous pouvons avoir une idée de leurs capacités d'attention ou leur mémoire immédiate par exemple. C'est ce que nous avons fait grâce à un échantillon de plusieurs milliers de volontaires. Ceux-ci ont entré des suites d'une dizaine de symboles (chiffres, dessins, cases dans un tableaux) qui leur semblaient aléatoires. Nous avons relevé la complexité des suites produites ainsi que la vitesse à laquelle les participants répondaient.
Résultats ? C'est à 25 ans que les suites sont le plus aléatoires, et aussi que l'on répond le plus vite. Entre 25 et 60 ans, la vitesse a tendance à diminuer, mais la complexité est presque stable, puis c'est la complexité qui s'effondre, plus que la vitesse. Il y a donc bien une évolution de la complexité, qui correspond à ce qu'on trouve aussi avec d'autres compétences cognitives générales comme l'intelligence ou la mémoire. Quand on regarde un peu plus dans le détail, on voit que ce que mesure la complexité n'est pas la même chose que ce que mesure la vitesse (elle aussi un indice global de fonctionnement cognitif). L'image animée en tête de ce billet permet de visualiser l'évolution simultanée de la complexité et de la vitesse : plus vous êtes en haut, plus vous êtes complexe. Plus vous êtes à gauche, plus vous êtes rapide.
Il s'agit bien sûr de moyennes (lissées, qui plus est) et il y a beaucoup de variabilité : vous pouvez tout à fait, à 70 ans, dépasser le niveau moyen des gamins de 25 ans... mais en moyenne, ce n'est pas le cas.
Références
Des comptes-rendus de notre article dans Scientific American, nzHerald et Cosmos Magazine.
-------------------------------------------------------------------------------------
Lorsque vous lancez deux dés, pensez-vous avoir plus de chance d’obtenir 11 ou 12 ? Ou bien les deux possibilités sont-elles aussi probables l’une que l’autre ?
À cette question, beaucoup de gens répondent que les deux sommes, 11 et 12, ont la même probabilité d’apparaître. Ils justifient cette intuition en disant que c’est le hasard qui détermine la somme et que le hasard ne favorise pas une alternative sur une autre. Or, 11 est en réalité deux fois plus probable que 12, parce que deux configurations (5-6 et 6-5) des dés correspondent à une somme de 11, alors qu’une seule (6-6) correspond à une somme de 12.
Cette erreur est nommée biais d’équiprobablité par les psychologues qui étudient cette question, l’équiprobabilité désignant le fait d’avoir des probabilités égales pour toutes les alternatives. Les psychologues ont très longtemps pensé que ce biais provenait d’une erreur conceptuelle fondamentale partagée par les humains selon laquelle le hasard est nécessairement équiprobable, alors que — selon leur théorie — ce n’est pas le cas.
Autrement dit, si on se trompe bien en pensant que 11 est aussi probable que 12, ce n’est pas à cause d’une conception fausse du hasard, mais parce qu’on pense à tort que le hasard peut se combiner. Selon l’analyse mathématique de la situation, si le nombre que donne chacun des deux dés est bien aléatoire, il n’en est pas de même de la somme ! Cet exemple révèle un paradoxe plus général : lorsqu’on combine des processus aléatoires (au sens mathématique), le résultat est en général non aléatoire, ce que nous avons appelé le paradoxe de la combinaison.
Pour le 421, il y a 6 manières de l'obtenir : 124 142 214 241 412 421. Donc oui, il est 6 fois plus probable que le triple 6 ou le triple 1.
'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
Pour calculer la probabilité de trouver 6 numéros au loto, il suffit de trouver combien il existe de séries non ordonnées de 6 nombres choisis parmi 49. On trouve :
(44 x 45 x 46 x 47 x 48 x 49) / (6 x 5 x 4 x 3 x 2)
soit 13 983 816. Ce calcul n'est
pas difficile. ______________________________________________
Inverser la martingale de Labouchère
Henry Labouchère était un politicien qui inventa une martingale que Norman Leigh eut l’idée d’inverser pour battre la roulette en jouant en équipe. En effet, dans un système de mises classique, le joueur augmente sa mise si il perd, améliorant ainsi les chances du casino : il s’agit ici de faire le contraire et de jouer systématiquement et simultanément sur le rouge et sur le noir, mais en jouant davantage sur la couleur qui sort que sur l’autre en augmentant sa mise quand il gagne et en la réduisant quand il perd.Le joueur mise alors réellement sur le fait qu’une roulette même parfaite ne produit pas exactement autant de rouge que de noir dans une même soirée. Ce système fonctionne dès qu’une couleur sort plus que l’autre. S’il y a exactement autant de rouge que de noir, le joueur ne gagne ni ne perd rien, si ce n’est lorsque le zéro sort, ce qui est peu par rapport aux gains.
Le système de mises de Norman Leigh, ou progression de Labouchère inversée, consiste pour le joueur à définir une série en début de partie, prenons les quatre nombres 1, 2, 3 et 4 dans cet ordre. Le joueur additionne les extrêmes, soit 1 + 4 = 5 et mise donc 5 unités sur une couleur, toujours la même. Lorsqu’il gagne, il recommence l’addition des extrêmes. S’il gagne tout de suite et continuellement, il joue 5, puis 6, puis 7, etc. S’il perd, il efface les nombres extrêmes et joue le dernier nombre non effacé de sa colonne, donc il joue moins que ce qu’il vient de perdre. Donc s’il perd tout de suite et continuellement, il joue 4, puis 3, etc.
Jeu en équipe avec le système de Labouchère pour battre la roulette
Norman Leigh jouait avec deux équipes de six joueurs qui se relayaient autour d’une même roulette, un joueur par bande. Chacun joue indépendamment, ils ne jouent donc pas en groupe, ils n’enfreignent pas cette règle du casino, par contre ils mettent le résultat de leur soirée au casino en commun, ce qui n’est pas interdit.
Jouer en équipe est indispensable pour couvrir toutes les bandes, un joueur seul ne peut arriver à faire ces calculs, ramasser les gains et placer ses mises pour chaque bande par lui-même le tout en moins de deux minutes : au casino, il y a au moins 30 tirages par heure.
Mais alors, comment se fait-il que les casinos existent encore ?
Il s’agit d’argent gagné péniblement, c’est un système extrêmement difficile à mettre en oeuvre et à suivre, en particulier dans la réalité, dans un vrai casino bondé où les distractions sont pléthoriques.
Cet article est inspiré de l’article « Labouchère est un bon coup » par Pierre Morichau (1967) de l’ENSAE (Ecole Nationale de la Statistique et de l’Administration Economique).
Avantages et risques
L’avantage de la stratégie Labouchère inversée est qu’elle permettrait de réduire le risque d’augmentation des mises suite à une grande série de pertes.Mais comme les cycles finissent sur des pertes, il n’est plus possible d’assurer un profit à chaque cycle. La succession des cycles perdant sur le long terme mène à un épuisement lent de la bankroll. Comme le montant perdu à chaque cycle est limité, il correspond à la somme totale de la mise (mise initiale).
Le choix de la séquence est très important dans une stratégie Labouchère inversée et il y a deux considérations importantes :
- Eviter les grands nombres pour limiter les pertes
- Utiliser plusieurs nombres, 6 au minimum pour faire durer le cycle à minima et garantir un minimum de gain avant la disparition du cycle
La Piquemouche
C'est une autre variante de la martingale classique. Le joueur recommence à une unité quand il gagne, mais quand il perd, il augmente sa mise d'une unité, il ne la double qu'après trois pertes consécutives. Elle ne nécessite pas d'augmenter dès le début les mises en cas de pertes successives, elle est plus sûre, mais les gains sont plus faibles (nuls si on ne gagne pas dès la première partie) ou nécessitent de gagner deux fois.
Exemple :
Le joueur mise une unité ; s'il gagne, il quitte le jeu avec 2 unités - 1 unité qu'il a jouée = 1 unité
S'il perd une première fois, il joue 1 unité ; s'il gagne, il emporte 2 unités - 1 (qu'il a jouée dans la 2e partie) - 1 (qu'il a jouée dans la 1re partie) = 0 unité
S'il perd une deuxième fois, il joue 1 unité ; s'il gagne, il emporte 2 unités - 1 (qu'il a jouées dans la 3e partie) - 1 (qu'il a jouée dans la 2e partie) - 1 (qu'il a jouée dans la 1re partie) = -1 unité
Il faut donc un deuxième gain pour être gagnant.
Suite de mise si toujours perdant 1 - 1 - 1 - 2 - 2 - 2 - 4 - 4 - 4 - 8 ...
etc.
______________________________________________________
Bonsoir Novocaine.
L'approche que j'ai développée est très rationnelle en effet, mais peut paraître "illogique". À chaque match, j'ai 2 chances sur 3 de ne pas perdre, peu importe le match, en DNB ou double chance. Après tout est question de cotes. Si la cote est proche de 2 pour la victoire à domicile et que les critères de base sont remplis, je joue "aveuglement" le match, tous championnats confondu, et sans poursuivre l'analyse, car ma gestion fait qu'une perte sera plus facilement compensée.
A l'inverse, plus la cote est faible et plus les critères sont déséquilibrés pour l'équipe 1, plus je creuse et poursuis l'analyse, car j'ai "plus à perdre" sur une petite cote. Dans ce cas- là, je ne laisse rien passer et termine par une analyse à la "Novocaine"... Différence home/away 5 derniers matchs d'au moins 8 points et au moins 10 matchs de championnats.
Si j'ai décidé de poster mes paris, c'est dans l'ambition de montrer (ou me prouver) que la méthode fonctionnerait pour tous les championnats et à n'importe quel moment de la saison. Ce n'est pas pour rien que j'ai commencé au mois de juin, à la fin des principaux championnats.
____________________________________________________
Loi de Dubins et Savage
Mathématiquement, Lester Dubins et Leonard Savage ont démontré en 1956 que la meilleure façon de jouer dans un jeu où les probabilités sont défavorables au joueur consiste à miser toujours ce qui permet d'approcher le plus rapidement le but visé. Intuitivement ce résultat semble évident : si à chaque partie on a plus de chances de perdre que de gagner, autant minimiser le nombre de parties jouées. Ce résultat signifie également qu'à moins de disposer d'une mise de départ infinie, il n'existe pas de stratégies permettant de renverser les probabilités en votre faveur dans un jeu qui vous est défavorable.Même dans le cas d'un jeu équitable, le joueur qui a à la fois la possibilité et la volonté de miser le plus se donne plus de chances de ruiner son adversaire et donc de l'empêcher de continuer à jouer : ainsi, au prix d'une perte potentielle plus grande, il se donne aussi plus de chance de gagner. Comme dans toute martingale, cela ne modifie toutefois pas l'espérance des deux joueurs (c'est-à-dire le plus « petit joueur » a moins de chance de gagner mais, aussi paradoxal que ça paraisse, il peut gagner plus !).
------------------------------------------------------------------------------------------------------------------
--Paul Lévy est un mathématicien français, né le 15 septembre 1886 à Paris où il est mort le 15 décembre 1971. Il figure, avec Émile Borel, Richard von Mises, Andreï Kolmogorov, Norbert Wiener, Joseph Leo Doob et Kiyoshi Itō, parmi les fondateurs de la théorie moderne des probabilités. On lui doit aussi des considérations importantes sur les lois stables stochastiques qui portent son nom ainsi que sur les martingales. --------------------------------------------------------------------------------------------------------------
En théorie des probabilités, la loi arc sinus est une loi de probabilité à densité dont le support est un intervalle compact. Elle est un cas particulier de la loi bêta
Une tentative d’explication au grand public d’une loi mathématique, qui s’appuie sur les élections et les sondages sortis des urnes lors de l’élection présidentielle de … 1967 ! Ici, le théorème de Paul Lévy, l’un des fondateurs de la théorie moderne des probabilités.
Le concept de martingale, prend sa source dans les jeux d'argent.Sur le plan étymologique, une martingale était une chaussure du 15è siècle (chausses à la martingale) de forme aberrante. Depuis le 18è siècle, dans les jeux d'argent, jouer une martingale consiste à jouer le double de la mise précédente tant que l'on a perdu, en espérant ainsi récupérer ses mises.
Un joli théorème de Levy relatif à la loi normale (1934), également dit de
Cramér-Levy :
|
Une variable aléatoire X pouvant
s'écrire comme somme Y + Z de deux variables indépendantes ne peut être
gaussienne (distribution de Laplace-Gauss, dite normale) sans que Y et Z ne le
soient.
Ce joli résultat, conjecturé par Lévy fut prouvé par Harald Cramer en
1936
Notion de martingale :
|
Le concept de
martingale, prend sa source dans
les jeux d'argent. Sur le plan étymologique, une martingale était une chaussure
du 15è siècle (chausses à la martingale) de forme aberrante. Depuis le 18è
siècle, dans les jeux d'argent, jouer une martingale consiste à jouer le double
de la mise précédente tant que l'on a perdu, en espérant ainsi récupérer ses
mises.
Très risqué ! Mais on est en effet
théoriquement sûr de récupérer sa mise, à condition d'avoir une
fortune illimitée !
Voyons cela : si la première mise m est perdue, on joue 2m. Si on gagne, tant mieux, sinon, on joue 4m et ainsi de suite. Si on gagne au n-ème jeu, la dernière mise n'est pas perdue car la perte de mise au coup k est 2k-1 x m. Le gain relatif est alors :2n-1 x m - (m + 2m + ... + 2n-2 x m) = 2n-1 x m - (1 + 2 + ... + 2n-2) x m = mcar la parenthèse est la somme des n - 1 premiers termes de la progression géométrique de raison 2, soit (1 - 2n-1)/(1 - 2) = 2n - 1 - 1.
Vous récupérez ainsi votre mise et le gain
associé au coup. Mais si vous n'êtes pas lourdement imposé à l'ISF, le pari reste très
risqué... D'une façon générale, une martingale est une stratégie
permettant d'augmenter ses gains dans un jeu de hasard.
---------------------------------------------------------------------------------------------------------------------
Pour pallier au problème des plafonds imposée par les casinos des petits génies ont alors pensé jouer à plusieurs, l’histoire la plus connue dans le domaine étant celle de Norman Leigh.
En 1966, Norman Leigh forme une équipe de douze joueurs et part à l’assaut des tables de roulette de Nice. Dans son livre Treize contre la banque, il fournit de nombreux détails sur le jeu de la roulette. Ecrit comme un roman, nombreux sont ceux qui ont pris cette histoire pour une œuvre de fiction : il n’en est rien ! Utilisant la technique de Labouchère inversée, ils ont fait, paraît-il, sauter la banque dans de nombreux casinos jusqu’à ce qu’ils soient détectés et bien évidement interdits de casino.
Technique de Labouchère :
L’idée est de déterminer la somme que vous souhaitez gagner, disons 20€ en 4 coups.
Vous partagez cette somme en 4 chiffres disons 4, 6, 5, 5 et vous vous obligez à ne parier que sur des paris simples ( noir ou rouge sinon pair -impair)
Vous partagez cette somme en 4 chiffres disons 4, 6, 5, 5 et vous vous obligez à ne parier que sur des paris simples ( noir ou rouge sinon pair -impair)
Pour le 1er tour, vous allez miser la somme du 1er et du dernier chiffre de cette liste
soit 4+5 = 9€.
Si vous gagnez, vous rayez ces chiffres et vous passez aux 2 suivants, soit le 2e et le 3e chiffre.
Si vous perdez, vous rajoutez les 9€ perdus au dernier chiffre de la liste et vous
soit 4+5 = 9€.
Si vous gagnez, vous rayez ces chiffres et vous passez aux 2 suivants, soit le 2e et le 3e chiffre.
Si vous perdez, vous rajoutez les 9€ perdus au dernier chiffre de la liste et vous
recommencez si bien que votre prochaine mise sera de 4 + (5+9) soit 17€.
Ainsi de suite!
Mais comme toutes les martingales, elle n’est pas infaillible, à vrai dire les seules méthodes infaillibles qui ne consistent pas à tricher, semblent avoir été liées au repérage de cylindres qui n’étaient pas parfaits. Les imperfections faisaient en sorte que certains chiffres tombaient plus souvent que les autres. Quelques perfectionnistes américains ont ainsi fait fortune. Mais cela n’est plus possible car les cylindres sont changés régulièrement et des tests ont été mis en place.
-----------------------------------------------------------------------------------------------------------------Dit plus trivialement, aucune martingale ne permet de modifier l’espérance mathématique d’un jeu de hasard, sauf à mettre une cale sous un pied de la table de roulette ou à augmenter le poids de certaines boules du loto, mais là il ne s’agit plus de martingale …
---------------------------------------------------------------------------------------------------------------------
Une martingale est une technique de jeu qui a pour but d'augmenter les chances de gain aux jeux de hasard. Il s’agit d’appliquer aux probabilités de gains des lois mathématiques plus ou moins complexes. La part de chance est ainsi réduite, tout en respectant les règles du jeu. Le principe de la martingale dépend du type de jeu qui en est la cible.
Malgré tout, ce type de technique ne change pas l'espérance du gain de l’utilisateur. En moyenne, un joueur utilisant une martingale ne gagnera pas plus qu'un joueur qui n’en utilise pas. Ces méthodes permettent de perdre moins souvent, mais elles augmentent en contrepartie le montant des pertes.
Il en existe beaucoup mais certaines sont plus connues que d’autres.
-----------------------------------------------------------------------------------------------------------------
La martingale américaine (« montante américaine »)
On l’appelle aussi « montante américaine ». Elle est assez compliquée.
- Le joueur commence par augmenter ses mises d'une unité tant qu'il gagne.
- Dès qu'il perd, il retient la mise qu'il vient de perdre. Il remise ensuite la somme de la dernière et de la première mise.
- Quand il gagne, il retient la mise qu'il vient de gagner et raye la première mise de sa liste. Puis il remise la somme de la dernière et de la première mise de sa liste, en ne tenant pas compte de celle qu'il a rayée.
-------------------------------------------------------------------------------------------------------------------
La martingale hollandaise
C’est une martingale utilisée en cas de pertes. Le joueur doit retenir les mises perdues, ce qui présente une difficulté par rapport à des martingales plus facilement utilisables. Voici le principe en supposant que le joueur a perdu plusieurs mises :
- Le joueur parie la mise la plus faible parmi celles qu'il a perdues + 1 unité de mise.
- Il mise ensuite la 2ème mise la plus faible, et ainsi de suite dans l'ordre croissant. A chaque victoire, le joueur gagne le montant d'une mise perdue précédemment, plus 1 unité de mise.
L’avantage de cette martingale est que si le joueur obtient autant de victoires que d'échecs, son gain reste positif si les coups gagnants surviennent après les coups perdants.
-------------------------------------------------------------------------------------------------------------------La « piquemouche »
C’est une autre variante de la martingale classique (ou martingale simple) mais plus complexe.
- Le joueur recommence à une unité quand il gagne.
- Il augmente sa mise d’une unité quand il perd.
- Il double sa mise à partir de trois pertes consécutives.
L’avantage est que cette martingale est plus sûre, mais en même temps les gains remportés sont plus faibles.
----------------------------------------------------------------------------------------------------------------------La « pyramide d’Alembert »
Le nom de cette martingale fait référence à M. Jean le Rond d'Alembert, mathématicien du 18ème siècle. Le principe est basé sur le fait que l’on pense qu’une perte augmente la chance de gagner la prochaine fois, et inversement.
- Le joueur augmente sa mise d'une unité après une perte.
- Il enlève une unité de mise après un gain.
Elle est moins dangereuse que la martingale simple. Même si les pertes sont parfois assez importantes, la pyramide d’Alembert permet d’enchaîner de plus longues séries.
---------------------------------------------------------------------------------------------------------------Le « paroli »
Il consiste à doubler sa mise à chaque gain, c’est-à-dire remiser ce que l’on a gagné.
L'avantage de cette « montante » est que l'on ne risque qu'une unité de son capital de départ à chaque fois. Le joueur joue ensuite avec l’argent du casino qu’il a gagné. Ses gains sont exponentiels. La somme remportée peut être conséquente en cas de plusieurs gains d’affilés. L'inconvénient en revanche est qu'un seul coup perdant suffit pour annuler tous les gains précédemment remportés.
--------------------------------------------------------------------------------------------------------------------La « whittacker »
Cette martingale est méconnue mais peut être intéressante.
- Le joueur mise la somme de ses deux précédentes mises tant qu’il perd.
- Il recommence à une unité de mise quand il gagne.
La whittacker permet un moindre coup de l’enchaînement des mises en cas de pertes successives. En revanche, un coup gagnant ne pourra contrer que deux coups perdants.
---------------------------------------------------------------------------------------------------------------_____________________________________________________________________
-
Le but des martingales et son « à priori » réussite
La martingale est le plus célèbre pari au monde. S’il existe différentes martingales, le principe de base ne change pas, et il faut se méfier de toutes.
Le but est de pouvoir inverser le taux de redistribution en faveur du joueur. Ce système de mises, que l’on appelle « martingales » ne paraît pas surprenant en soi… au contraire, cela parait plutôt logique ! Mais les apparences sont parfois trompeuses, et les martingales dangereuses car leur principe est défaillant. Malgré les avertissements et les démonstrations à l’appui, de nombreuses personnes pensent encore que ce système st efficace. Au départ, elle a été crée pour des jeux comme le Blackjack ou encore la roulette. Son principe est simple, en doublant la mise perdue à chaque nouveau pari, on est forcément gagnant en théorie.
Le phénomène des martingales a donné lieu à un article rédigé par un professeur de mathématiques. Il s’agit de l’ouvrage « Les martingales et autres illusions », publié dans le magazine « La science » en 1998, après avoir étudié des milliers et des milliers de mains.
----------------------------------------------------------------------------------------------------------
roduire un hasard parfait avec une absolue certitude est difficile ; au sens mathématique, c’est même impossible. Cependant, on admet que les méthodes à base de mécanique quantique créent un hasard probablement correct, et même que certaines méthodes purement algorithmiques donnent des séquences aléatoires si proches du hasard parfait qu’on peut les utiliser en toute tranquillité.
Nous examinerons ici la création sécurisée d’aléas publics et la mise à disposition d’un hasard infalsifiable, utile dans de nombreuses situations. Cette création de hasard sera le fait de balises aléatoires (en anglais : random beacons), des phares numériques émettant des nombres (binaires ou autres) aléatoires que tout le monde peut voir et que nul ne peut fausser et anticiper. On utilise parfois le terme « source publique d’aléas », mais nous préférerons le terme de balise aléatoire.
Si un site de jeux sur internet prétend tirer seul au hasard les gagnants d’une loterie ou distribuer des cartes à partir d’un jeu bien mélangé, il n’est pas raisonnable de lui faire confiance, car il peut faire gagner qui il veut et manipuler les distributions de cartes… et cela s’est déjà produit. En revanche, s’il indique précisément comment, à partir d’une balise aléatoire sûre et indépendante, il déduit les gagnants ou obtient le mélange du jeu de cartes, et que chacun peut vérifier qu’il respecte le protocole fixé, il ne pourra pas tricher.
Il en va de même plus généralement pour tous les sites internet qui proposent des jeux où le hasard intervient, et cela concerne aussi les loteries nationales, lotos et autres jeux d’argent organisés à grande échelle. Tous devraient proposer des procédures de tirage non plus fondées sur des dispositifs physiques locaux que certains ont su manipuler, mais sur des balises aléatoires sécurisées dont l’utilisation serait rendue parfaitement contrôlable a posteriori grâce aux données enregistrées.
L’utilisation de balises aléatoires concerne d’autres domaines et devrait y être obligatoire. Si une entreprise qui produit des médicaments assure qu’elle teste au hasard les lots mis en circulation, il est souhaitable que le système de tirage au sort qu’elle utilise pour ces contrôles soit fondé sur un tirage aléatoire extérieur, car c’est la seule façon d’être certain que l’entreprise ne choisisse pas les cobayes à sa convenance.
------------------------------------------------------------------------------------------
1. Impossible hasard parfait
Les méthodes algorithmiques de production de suites aléatoires ne donnent pas des suites aléatoires au sens fort défini par Per Martin-Löf en 1965. En effet, « être produit par un algorithme » entraîne que celui qui détient l’algorithme peut anticiper ce qui sera produit. De plus, ce qui est produit par un algorithme peut être compressé en un fichier de taille au plus égale à la taille du programme de l’algorithme ; or ce qui est authentiquement aléatoire est incompressible. Les décimales de ≠, en particulier, sont produites par des algorithmes tirés de séries numériques classiques et ne constituent donc pas une suite aléatoire au sens fort.
Les méthodes physiques (loterie, bruit thermique, mécanique quantique, etc.) ne produisent des suites aléatoires au sens fort que (1) sous l’hypothèse que les théories associées (par exemple la mécanique quantique) sont les bonnes théories qui régissent la physique du mécanisme producteur, ce qui est impossible à prouver, et (2) si le dispositif physique producteur a été correctement monté et ne subit aucune manipulation, et en particulier n’est victime d’aucune porte dérobée. Il se peut donc que les méthodes quantiques produisent de véritables suites aléatoires, mais l’affirmer est impossible car cela reviendrait à affirmer que la mécanique quantique est une théorie qui ne sera jamais remise en cause, et que l’on a bien modélisé le dispositif physique utilisé, deux affirmations risquées, comme le montre l’histoire de la physique.
---------------------------------------------------------------------------------------------------------
La météo, une balise aléatoire ?
Notre premier exemple de balise élémentaire donnant un aléa public pour le pile ou face par téléphone s’appuie sur la météo. La balise serait déduite des publications sur internet de Météo-France. Elle produirait un bit par jour en se fondant sur la température à midi relevée par Météo-France à la station météorologique de Paris-Montsouris. Cette température serait arrondie au dixième de degré inférieur et un 0 (correspondant à pile) serait produit si le premier chiffre après la virgule de la température est pair et un 1 (correspondant à face) serait produit si le premier chiffre est impair.
Un site internet donne cette température « officielle » et peut donc, sans intermédiaire, servir de balise aléatoire : www.infoclimat.fr/observations-meteo/temps-reel/paris-montsouris/07156.html. La température à midi y est chaque jour définitivement inscrite sur le site et reste ensuite accessible. On trouve par exemple les données suivantes : 11,8 °C pour le 28 novembre 2019 à midi, qui donnerait un 0, donc pile ; 9,5 °C pour le 29 novembre 2019 à midi, qui donnerait un 1, donc face ; 7,8 °C pour le 30 novembre 2019 à midi, qui donnerait un 0, donc pile ; 3,5 °C pour le 1er décembre 2019 à midi, qui donnerait un 1, donc face ; 5,2 °C pour le 2 décembre 2019 à midi, qui donnerait un 0, donc pile. La suite des tirages est donc, à partir du 28 novembre : pile-face-pile-face-pile. On peut opérer un tirage à pile ou face par téléphone tous les jours à midi.
----------------------------------------------------------------------------------------------------
Cette balise est très probablement aléatoire : il n’y a aucune raison de penser que les nombres pairs (ou impairs) soient favorisés, ni qu’aucune séquence particulière de pile ou face soit plus fréquente qu’une autre de même longueur. Elle est bien imprévisible, car les prévisions météorologiques pour Paris ne sont pas assez précises pour qu’on puisse savoir à l’avance ce qui va venir comme premier chiffre après la virgule de la température à midi. La balise est vérifiable a posteriori : tout le monde peut aller consulter le site mentionné pour voir ce qui y est indiqué. On peut raisonnablement faire confiance au sérieux des opérateurs du site pour qu’ils ne changent pas les données inscrites et qu’ils les maintiennent accessibles assez longtemps.
Trois problèmes persistent cependant avec cet aléa public.
(1) Prévoir le résultat du tirage devient possible quand on s’approche de midi, car la température varie continûment. Il faudrait donc convenir au moins quelques heures avant midi que l’on va jouer à pile ou face et attendre midi pour que s’effectue le tirage.
(2) Le procédé n’est pas rapide. En considérant d’autres lieux de relevé, d’autres heures, d’autres données (pression, hygrométrie, etc.) on pourrait faire mieux, mais on resterait limité à quelques bits par minute au plus.
(3) Peut-on faire totalement confiance à ce qui est publié par le site de Météo-France ? Est-ce qu’il ne se pourrait pas qu’un employé, par négligence, erreur de manipulation ou soudoyé par l’un des joueurs, modifie le relevé publié pour produire des températures autres que celles vraiment relevées ? L’un des joueurs ne pourrait-il pas s’introduire sur le site et en modifier les chiffres publiés ? Nous verrons par la suite que nous pouvons pallier cette incertitude sur la stabilité et la sécurité de ce qui est inscrit.
Les cours de bourses, les taux de change, les résultats sportifs, le contenu de ce qui est publié par les médias (journaux, radio, télévisions, pages web), sont d’autres sources publiques d’aléas et vérifiables a posteriori. Certaines sont assez rapides, mais aucune ne donne une assurance de stabilité supérieure aux données publiées par Météo-France. Avec elles, on aura donc en définitive un aléa public ayant les mêmes imperfections qu’avec Météo-France.
--------------------------------------------------------------------------------------------------------------------
Autres sources partageables d’aléas
Conscients de l’intérêt de disposer de meilleures sources publiques d’aléas, certains sites internet en proposent. Ainsi, le site random.org rend disponible des nombres aléatoires de toutes sortes depuis 1998.
Ce site, conçu et réalisé par Mads Haahr, du Trinity College, à Dublin, propose des nombres aléatoires qu’il qualifie de « véritables », car tirés du bruit atmosphérique capté par radio. On peut par exemple obtenir, à la demande, le résultat d’un lancer de deux dés, ou le mélange d’un paquet de 52 cartes, ou même une image aléatoire faite de pixels noirs et blancs.
Random.org affirme extraire 12 000 bits par seconde du bruit atmosphérique, et c’est à partir d’eux que les autres services sont fournis. Si on le souhaite, les nombres que le site communique sont mémorisés, mais ce n’est pas très facile car le site n’est pas conçu pour jouer le rôle de balise aléatoire sécurisée émettant périodiquement. Par ailleurs, on ne sait pas vraiment comment le bruit atmosphérique est capté et transformé en données aléatoires. Utiliser random.org pour les applications n’exigeant pas une certitude d’honnêteté et de sécurité totale sera une assez bonne solution, mais, tel qu’il est conçu, ce site internet n’est pas en mesure de fournir assez de garanties pour des applications où par exemple des sommes importantes d’argent seraient en jeu.
La balise du Nist : une liste de 512 bits chaque minute
C’est sans doute pourquoi l’institut américain des normes et de la technologie, le NIST (National Institute of Standards and Technology), travaille sur ce problème depuis 2011 et propose une balise aléatoire, conçue cette fois comme un émetteur public et périodique d’aléas dont les données produites sont protégées et restent consultables sans limitation de temps. La balise du NIST publie chaque minute une liste de 512 bits aléatoires (voir https://beacon.nist.gov/home). Et le NIST encourage la création d’autres balises indépendantes.
Le NIST utilise les bits émis par un dispositif quantique. Il fournit un moyen de vérifier que les bits publiés ne sont pas modifiés une fois publiés et affirme que son site est protégé contre toute intervention extérieure, ce qui assure que personne ne manipule le mécanisme de production ou de publication.
Si l’on considère que le NIST est un tiers de confiance parfait, on peut utiliser ce qu’émet sa balise. Par exemple, si des sites de jeux qui utilisent des nombres aléatoires vont les y rechercher en indiquant comment, on pourra avoir confiance en eux et vérifier qu’il n’y a pas tricherie, car il est improbable que le NIST se laisse corrompre par eux. Malgré tout, comme le notent de nombreux spécialistes, le NIST ne donne aucun moyen pour contrôler que les bits qu’il publie sont produits par des phénomènes quantiques et qu’aucune manipulation n’est opérée par l’institut sur ce qu’il émet. Le NIST ayant déjà été soupçonné de tentatives de trucage liées à des outils de génération d’aléas (voir https://en.wikipedia.org/wiki/Dual_EC_DRBG), il est impossible de recommander d’utiliser sa balise pour les applications exigeant une sécurité absolue.
Remarquons que, sur sa page, le NIST indique en rouge qu’il ne faut pas utiliser sa balise pour choisir des mots de passe. La recommandation est tout à fait justifiée et s’applique à tous les générateurs publics d’aléas. En effet, les données publiées restent accessibles (c’est nécessaire pour mener des contrôles a posteriori), ce qui signifie que si votre mot de passe a été engendré par une balise publique, quelqu’un cherchant à le deviner a accès aux mêmes nombres aléatoires, ce qui facilite son travail. Pour vos mots de passe, utilisez des générateurs privés et si possible indépendants de votre machine !
D’autres sites se présentent comme des balises aléatoires sécurisées et réussissent à faire mieux que la balise du NIST.
Le Laboratoire de sécurité computationnelle et de cryptographie appliquée de l’université du Chili (https://random.uchile.cl/en/) propose une balise dont les bits dépendent à la fois d’une source quantique locale et de données extérieures (données sismiques, radio de l’université du Chili, blockchain Ethereum, Twitter). Ce site est l’une des meilleures balises actuelles : il utilise le principe décrit plus loin et dans l’encadré 3.
Le site brésilien d’Inmetro, l’Institut national de la métrologie et de la qualité (www4.inmetro.gov.br/) et le projet collaboratif League of entropy (www.cloudflare.com/leagueofentropy/) offrent divers outils de génération de hasard privé et public. Là encore, ils s’appuient sur des méthodes cryptographiques avancées pour sécuriser les émissions.
Les balises évoquées sécurisent et améliorent la vérifiabilité a posteriori de leurs émissions. Quelles sont les méthodes mises en œuvre ?
Garantir l’impossibilité de modification
La première idée est la signature. Les données aléatoires produites peuvent être signées par un procédé cryptographique qui assure que ce qu’on lit sur le site internet n’a pas été écrit ou réécrit par un autre acteur que le site producteur. Les signatures numériques sont vérifiables par tous, mais seul l’organisme producteur (qui indique sa clé publique permettant le contrôle) peut (grâce à sa clé privée) produire les signatures.
Pour garantir que les nombres publiés ne soient pas modifiés après coup, on peut utiliser une fonction de hachage. En même temps que la balise aléatoire publie le k-ième nombre aléatoire Nk, elle publie un autre nombre Ek qui est l’« empreinte », par une fonction de hachage cryptographique, de Ek – 1 Nk (la concaténation de Ek – 1 et de Nk). Cette publication lie toutes les publications antérieures, car la publication à l’étape k dépend de celle à l’étape k – 1, qui elle-même dépend de la publication à l’étape k – 2, etc. Le procédé rend visible toute modification qui serait apportée aux Nk après leur publication.
_________________________________________________________________________
---------------------------------------------------------------------------------------------------
De droite à gauche, trois des plus grands génies du XXe siècle : Stanislaw Ulam, Richard Feynman et John von Neumann. Ulam et von Neumann comptent parmi les pionniers de l'utilisation des ordinateurs en physique et en mathématiques, notamment avec l'utilisation de générateurs de nombres pseudo-aléatoire et la méthode de Monte Carlo. Feynman est lui l'un des premiers contributeurs à la théorie des ordinateurs quantiques.
_____________________________________________________________________
_________________________________________________________________________
---------------------------------------------------------------------------------------------------
Pour choisir aléatoirement un nombre entre 0 et 1.024, une idée est de jouer dix fois à pile ou face. En notant 0 les piles et 1 les faces, nous obtenons un nombre à dix chiffres binaires, comme par exemple 1001011111 (que nous avons effectivement trouvé ainsi). En décimal, cela donne 1+2+4+8+16+64+512, soit 607. Bien entendu, si on joue onze fois à pile ou face, on obtient un nombre entre 0 et 2.048, etc.
Dans plusieurs domaines des mathématiques (simulation, calcul scientifique, cryptographie), on a besoin d'une grande quantité de nombres aléatoires donc de suite de tels nombres. La méthode que nous venons de proposer devient vite impraticable.
La création du pseudo-aléatoire
Il est plus économique d'utiliser une suite déterministe ayant les apparences d'une suite aléatoire. Voici une recette pour en fabriquer une, de nombres entre 0 et 2147483646. On prend un premier terme réellement au hasard, par exemple l'heure en nanosecondes, qu'on appelle le germe, disons 3248455607. On multiplie ce nombre par 16807 et on garde le reste du résultat dans la division par 2147483647. On obtient 1316629168. On recommence la même opération avec ce nouveau nombre et ainsi de suite : 914927888, 1210101096, 1498983382, 1283038317, etc. Cette suite ressemble à une suite aléatoire, elle passe tous les tests usuels de répartition des suites aléatoires mais elle est pourtant déterministe.
Utilisation
Quand l'important est d'utiliser une suite de nombres équirépartis sur un intervalle donné, le pseudo-aléatoire peut remplacer l'aléatoire sans problème. Quand l'important est que les termes de la suite soient imprévisibles, ce n'est pas le cas. Dans la première catégorie, on trouve les utilisations en simulation et en calcul numérique, dans la seconde, les utilisations en cryptographie.
_________________________________________________________________De droite à gauche, trois des plus grands génies du XXe siècle : Stanislaw Ulam, Richard Feynman et John von Neumann. Ulam et von Neumann comptent parmi les pionniers de l'utilisation des ordinateurs en physique et en mathématiques, notamment avec l'utilisation de générateurs de nombres pseudo-aléatoire et la méthode de Monte Carlo. Feynman est lui l'un des premiers contributeurs à la théorie des ordinateurs quantiques.
_____________________________________________________________________
Parler de science du hasard semble résonner comme un oxymoron mais cela n'a pas empêché mathématiciens, physiciens et philosophes, comme Pascal, Laplace et Cournot d'analyser le concept de hasard et son rôle dans la nature depuis des siècles. Ce dernier a été à l'origine de la théorie des probabilités que l'on utilise lourdement en mécanique statistique, pour décrire les fluides turbulents, et bien sûr en mécanique quantique.
Le grand mathématicien russe Kolmogorov a finalement donné une théorie axiomatique du calcul des probabilités en 1933. Le grand philosophe Karl Popper a lui beaucoup réfléchi sur le statut exact du hasard et des probabilités en épistémologie et en ce qui concerne les lois de la nature dans ses deux célèbres ouvrages La logique de la découverte scientifique et L’Univers irrésolu, plaidoyer pour l’indéterminisme.
Des nombres aléatoires pour la physique et la cryptographie
Au cours du XXe siècle on a tenté d'apprivoiser et d'utiliser le hasard avec ce qu'on appelle des générateurs de nombres pseudo-aléatoires. Grossièrement parlant, des générateurs de nombres pseudo-aléatoires sont des algorithmes qui génèrent des suites de nombres semblant suffisamment désordonnés et différents les uns des autres pour que l'on puisse croire, sans un examen rigoureux, qu'ils ont été tirés au hasard. L'un de ces générateurs les plus célèbres a été découvert en 1946 par John von Neumann. Il est connu sous le nom de la méthode middle-square (carré médian). On en utilise des biens plus sophistiqués depuis lors. Ils permettent de mettre en pratique dans de nombreuses sciences la puissante méthode de l'algorithme de Monte-Carlo.
Les générateurs de nombres pseudo-aléatoires sont aussi très importants pour faire de la cryptographie, qu'elle soit classique ou quantique. Ils permettent donc de sécuriser des transactions bancaires et de transmettre des messages secrets entre des États ou des armées. Toutefois, comme leur non l'indique, les générateurs de nombres pseudo-aléatoires ne produisent pas vraiment des suites de nombres tirés au hasard car ces nombres dérivent de processus mathématiques et déterministes. Il existe donc une certaine vulnérabilité des codes secrets basés sur l'emploi de ces suites qui ne sont en réalité pas aléatoires au sens exact du terme
La solution est connue depuis longtemps. Au lieu d'utiliser les mathématiques on recourt à la physique. Les fluctuations statistiques des désintégrations radioactives en mécanique quantique ou les fluctuations statistiques thermiques des courants d'électrons dans un dispositif électronique produisent un signal bruité que l'on peut considérer comme vraiment aléatoire. Malheureusement, il peut être difficile de mettre en pratique ces générateurs et surtout, bien souvent, ils ne permettent pas de produire la quantité de nombres aléatoires demandée.
Du bruit quantique mesuré avec un smartphone
Des chercheurs de l'université de Genève, parmi lesquels Nicolas Gisin, bien connu pour ses travaux sur la cryptographie et la téléportation quantique, viennent d'avoir une brillante idée, c'est le cas de le dire, pour contourner cet obstacle, comme ils l'expliquent dans un article déposé sur arxiv. Ils se sont aperçus qu'ils pouvaient créer un générateur quantique de nombres aléatoires (quantum random-number generator ou QRNG) simplement en utilisant l'appareil photo à 8 mégapixels du smartphone Nokia N9.
Whidarte Joël
----------------------------------------------------------
Article le poids de la grille au LOTO
____________________________________
Arret optimal
Comment optimiser ses gains aux jeux de hasard ? Selon les mathématiciens, en s'arrêtant au bon moment. Les stratégies d'arrêt optimal s'appliquent à de multiples domaines : les marchés boursiers, l'évaluation des options financières, ou encore l'exploitation des ressources pétrolières.
Pour illustrer comment fonctionne la théorie de l’arrêt optimal, le chercheur utilise la comparaison suivante : « Imaginez que vous observiez l’évolution d’un cours boursier. Vous cherchez à savoir quand acheter ou quand vendre vos actions pour réaliser des bénéfices. Ce qu’il faut surveiller, c’est le "point de changement", c’est-à-dire le moment où un changement se produit dans les caractéristiques du cours de l’action. De cette manière, vous serez en mesure de réagir rapidement et de gagner de l’argent. Grâce à la théorie de l’arrêt optimal, il est possible de déduire le moment où se produit ce point de changement en surveillant et en examinant les données du marché au fur et à mesure.
____________________________________
L’aléa joue un rôle déterminant dans des contextes variés et il est souvent nécessaire de le prendre en compte dans de multiples aspects des sciences de l’ingénieur, citons notamment les télécommunications, la reconnaissance de formes ou l’administration des réseaux. Plus généralement, l’aléa intervient aussi en économie (gestion du risque), en médecine (propagation d’une épidémie), en biologie (évolution d’une population) ou en physique statistique (théorie des transitions de phases). Dans les applications, les données observées au cours du temps sont souvent modélisées par des variables aléatoires corrélées dont on aimerait prédire le comportement. L’objet de ce cours est de formaliser ces notions en étudiant deux types de processus aléatoires fondamentaux en théorie des probabilités : les chaînes de Markov et les martingales. Des applications variées seront présentées pour illustrer ces concepts.
"Promenade aléatoire: chaînes de Markhov et martingales", Thierry Bodineau (2013)
_____________________________________
Whidarte Joël
La méthode miracle universelle.
Les dessous du hasard.
La Roulette décriptée.
Le hasard nomenclaturé.
L'ordre caché du désordre.
Impossible n'est pas hasard !
La formule aléatoire.
La valeur absolue du hasard.
Un hasard borné.
La dépendance des systèmes aléatoires.
----------------------------------------------------------
Article le poids de la grille au LOTO
____________________________________
Arret optimal
Comment optimiser ses gains aux jeux de hasard ? Selon les mathématiciens, en s'arrêtant au bon moment. Les stratégies d'arrêt optimal s'appliquent à de multiples domaines : les marchés boursiers, l'évaluation des options financières, ou encore l'exploitation des ressources pétrolières.
Pour illustrer comment fonctionne la théorie de l’arrêt optimal, le chercheur utilise la comparaison suivante : « Imaginez que vous observiez l’évolution d’un cours boursier. Vous cherchez à savoir quand acheter ou quand vendre vos actions pour réaliser des bénéfices. Ce qu’il faut surveiller, c’est le "point de changement", c’est-à-dire le moment où un changement se produit dans les caractéristiques du cours de l’action. De cette manière, vous serez en mesure de réagir rapidement et de gagner de l’argent. Grâce à la théorie de l’arrêt optimal, il est possible de déduire le moment où se produit ce point de changement en surveillant et en examinant les données du marché au fur et à mesure.
____________________________________
Problème du secrétaire
Le problème de la secrétaire, du secrétaire ou des secrétaires est un problème mathématique de théorie de l’arrêt optimal en théorie de la décision, en théorie des probabilités et en statistique. Le problème est aussi connu sous le nom de problème de la princesse[1], et de problème du recrutement immédiat[2].
Le but est de définir une stratégie qui maximise la probabilité d'engager le meilleur candidat.
Le problème peut être vu comme un problème algorithmique, dans le contexte des algorithmes onlines.
A

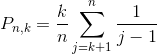
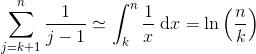
Problème du secrétaire
Sommaire
8,23 €
Retired Secretary Not My Problem Anymore: Secretary Dot Grid Notebook, Planner or Journal | Size 6 x 9 | 110 Dotted Pages | Office Equipment, Supplies ... Secretary Gift Idea for Christmas or Birthday
65,94 €
Plantronics C565 Kits Oreillette UHF Numérique, Connexion Sans Fil, [Utilisation possible uniquement avec téléphone DECT compatible GAP]
38,99 €
Esolom Casque Bluetooth avec Micro sans Fil,Casque avec Base de Charge,Casque Téléphonique,Casque PC Professionnel pour Annulation de Bruit,Mains Libres,Call Center,Conducteur de Camion
24,57 €
LSJTZ 2016, Hilary Rick, secrétaire d'Etat, Peint, Insigne, plaqué Argent, Antique, pièce commémorative, de Haute qualité, Cadeau
21,99 €
Contacts Cuir véritable Femmes secrétaire chéquier Titulaire de téléphone Longue Fermeture à glissière Portefeuille (Vert)
15,79 €
Boucles D'Oreilles Petites Boucles D'Oreilles De Secrétaire En Or Avec Boucles D'Oreilles Féminines
28,99 €
Feagar Coussin de Siège en Mousse à Mémoire, Coussin Orthopédique Coccyx Sciatique Soulager les douleurs, Ergonomique Coussin Anti Escarres pour Chaise Bureau Auto Voiture Fauteuil Roulant, Noir
17,95 €
Gants de Compression Supérieur Doigts Ouverts, Développés par des Médecins avec son Manuel (Gris/S)
24,99 €
WILIT HZ T3 5W Lampe de Table Dimmable, Lampe de Bureau LED, Lampe de Chevet pour Enfants, Champ Tactile pour la Lumière de Couleur et 3 Niveaux de Luminosité, Confortable pour les Yeux, Blanc
34,50 €
Adiggy Medical | Coussin anti escarres viscoélastique avec housse antidérapante en polyuréthane (PU) | Taille : 42x42x7 cm
17,95 €
Réglette LED Orientable avec Interrupteur, Luminaire Sous Meuble Lumière Réglables pour Cuisine/Armoire/Placard/Escalier/Couloir 3000K 4000K 6000K (Court)
Maîtrisez l’anglais en 12 sujets: Plus de 200 mots et phrases intermédiaires expliqués (English Edition)
11,99 €
Captain Marvel Vol. 1: Higher, Further, Faster, More (Captain Marvel (2014-2015)) (English Edition)
10 Rules for Achieving English Fluency: Learn how to successfully learn English as a foreign language (English Edition)
En tant que Partenaire Amazon, nous réalisons un bénéfice sur les achats remplissant les conditions requises.
Énoncé
Le contexte est le suivant : quelqu'un veut recruter un ou une secrétaire et voit défiler un nombre fini et connu de candidats. Pour chacun, il doit décider s'il l'engage ou pas. Si oui, il termine le processus de recrutement sans voir les autres candidats. Sinon, il n'a pas la possibilité de rappeler la candidate plus tard[3]. Dans le contexte de ce problème, le recruteur n'a pas accès à une valeur intrinsèque des candidats (comme « ce candidat vaut 7/10 » ), il ne peut que les comparer (par exemple «ce candidat est meilleur que le premier, mais moins bon que le deuxième »)[3].Le but est de définir une stratégie qui maximise la probabilité d'engager le meilleur candidat.
Le problème peut être vu comme un problème algorithmique, dans le contexte des algorithmes onlines.
Stratégie
La bonne stratégie[4] est de laisser passer 37 % des candidates (ou, plus précisément, une proportion 1/e), puis d'attendre d'avoir une candidate meilleure que toutes celles de ce premier échantillon[3]. On parle parfois de la règle des 37 %[1].
A
__________________________________
Le problème des secrétaires
En bon chef d'entreprise que vous êtes, vous avez décidé d'engager un (et un seul) nouveau secrétaire. Vous organisez donc une série d'entretiens, où n candidats se présentent (vous connaissez à l'avance ce nombre n de postulants). Les candidats seront interviewés tour à tour, l'ordre étant aléatoire. A l'issue de chaque entrevue, vous n'avez que deux possibilités : le candidat est embauché ou bien rejeté. S'il est embauché, vous ne poursuivez pas les entretiens ; si il est rejeté, vous n'aurez plus l'occasion de le revoir. Attention : si vous rejetez tous les candidats, vous devrez impérativement garder le dernier (La France est en crise, il faut réduire le chômage, quitte à embaucher n'importe qui). La question est donc : à quel moment est-il préférable d'arrêter les entretiens ?
En bon chef d'entreprise que vous êtes, vous avez décidé d'engager un (et un seul) nouveau secrétaire. Vous organisez donc une série d'entretiens, où n candidats se présentent (vous connaissez à l'avance ce nombre n de postulants). Les candidats seront interviewés tour à tour, l'ordre étant aléatoire. A l'issue de chaque entrevue, vous n'avez que deux possibilités : le candidat est embauché ou bien rejeté. S'il est embauché, vous ne poursuivez pas les entretiens ; si il est rejeté, vous n'aurez plus l'occasion de le revoir. Attention : si vous rejetez tous les candidats, vous devrez impérativement garder le dernier (La France est en crise, il faut réduire le chômage, quitte à embaucher n'importe qui). La question est donc : à quel moment est-il préférable d'arrêter les entretiens ?
Pour faire le meilleur choix, vous ne pouvez vous baser que sur un seul critère : le candidat est-il oui ou non meilleur que tous ses prédécesseurs (on suppose ici que l'on peut classer l'ensemble des postulants du moins bon au meilleur, sans ex aequo possibles). Mais comment peut-on faire pour maximiser les chances de tomber sur LE meilleur des candidats ?
La modélisation du problème est critiquable : un bon responsable des ressources humaines se gardera toujours la possibilité de rappeler un candidat après interview ("on vous rappellera"). De plus, il s'agit rarement de trouver le meilleur candidat, mais celui qui est qualifié pour le poste, quitte à ne garder au final aucun candidat. De plus, on peut imaginer que tous les candidats ne sont pas comparables deux à deux. Le problème des secrétaires connaît de très nombreuses variantes prenant ou non en compte ces objections, ce qui fait que le problèmes d'arrêt optimal forment une catégorie de problèmes particulièrement étudiés.
Cas n = 4
Prenons un premier exemple, avec n = 4 candidats : A (d'un niveau assez bon), B (d'un bon niveau), C (niveau très bon) et D (niveau excellent). L'objectif est donc de choisir D.
L'ordre étant aléatoire, on dénombre 24 possibilités : ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB et DCBA.
Prenons un premier exemple, avec n = 4 candidats : A (d'un niveau assez bon), B (d'un bon niveau), C (niveau très bon) et D (niveau excellent). L'objectif est donc de choisir D.
L'ordre étant aléatoire, on dénombre 24 possibilités : ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB et DCBA.
Stratégie 0 : Une première stratégie envisageable est de choisir le premier candidat, quoi qu'il arrive. On obtient alors une stratégie qui fonctionne avec une chance sur 4 (25%).
Stratégie 1 : Une autre stratégie envisageable est de s'entrenir avec le premier candidat, sans le garder. Ensuite, on gardera le premier des candidats à se présenter qui sera meilleur que le candidat n°1. Plusieurs cas sont envisageables :
- le premier candidat est D : il sera éliminé, tant pis.
- le premier candidat est C : le seul candidat meilleur que C est D, qui sera donc forcément choisi quand il se présentera -> 6 possibilités sur 24
- le premier candidat est B. Sous cette condition, on prendra le premier des candidats C ou D à se présenter -> 3 possibilités sur 24
- le premier candidat est A. Sous cette condition, le candidat n°2 sera choisi, soit une chance sur trois de tomber sur D -> 2 possibilités sur 24.
Au final, cette stratégie donne 11 chances sur 24 (46% de chances) de tomber sur D, le meilleur candidat. On peut aussi vérifier que l'on choisira C avec une probabilité de 7/24, B avec une probabilité de 4/24 et A avec une probabilité de 2/24.
- le premier candidat est D : il sera éliminé, tant pis.
- le premier candidat est C : le seul candidat meilleur que C est D, qui sera donc forcément choisi quand il se présentera -> 6 possibilités sur 24
- le premier candidat est B. Sous cette condition, on prendra le premier des candidats C ou D à se présenter -> 3 possibilités sur 24
- le premier candidat est A. Sous cette condition, le candidat n°2 sera choisi, soit une chance sur trois de tomber sur D -> 2 possibilités sur 24.
Au final, cette stratégie donne 11 chances sur 24 (46% de chances) de tomber sur D, le meilleur candidat. On peut aussi vérifier que l'on choisira C avec une probabilité de 7/24, B avec une probabilité de 4/24 et A avec une probabilité de 2/24.
Stratégie 2 : Une autre stratégie envisageable est de s'entrenir avec les deux premiers candidats sans les garder, puis de choisir le candidat n°3 s'il est meilleur que les deux premier, et le n°4 sinon.
Dans ce cas, D sera choisi systématiquement si les premiers candidats sont AC, BC, CA ou CB. Si les premiers candidats sont AB ou BA, D sera choisi dans la moitié des cas. Sinon, c'est que D est parmi les deux premiers candidats, et donc éliminé. On en déduit alors que D sera choisi avec une probabilité de 10/24 (soit 42%). Pour C, la probabilité est de 6/24, pour B et A, elle est de 4/24.
Dans ce cas, D sera choisi systématiquement si les premiers candidats sont AC, BC, CA ou CB. Si les premiers candidats sont AB ou BA, D sera choisi dans la moitié des cas. Sinon, c'est que D est parmi les deux premiers candidats, et donc éliminé. On en déduit alors que D sera choisi avec une probabilité de 10/24 (soit 42%). Pour C, la probabilité est de 6/24, pour B et A, elle est de 4/24.
On peut oublier la stratégie 3 consistant à ne pas sélectionner les trois premiers candidats pour ne garder que le dernier, qui fait retomber la probabilité d'embaucher D à 1 chance sur 4.
En appelant "stratégie k" la stratégie consistant à faire passer les k premiers candidats sans les garder, puis sélectionner le premier des candidats meilleur que ces k premiers, on vient de vérifier que dans le cas n = 4, la stratégie optimale est la stratégie 1. Le meilleur des candidats sera sélectionné avec une probabilité d'environ 46%.
Cas n = 5On peut procéder à la même analyse pour le cas n = 5, en envisageant les 120 ordres possibles pour 5 candidats. Les probabilités d'obtenir le meilleur candidat, suivant les différentes stratégies envisageables, sont alors :
Stratégie 0 : p = 20 %
Stratégie 1 : p = 41.7 %
Stratégie 2 : p = 43,3 %
Stratégie 3 : p = 35 %
Stratégie 4 : p = 20 %
Stratégie 1 : p = 41.7 %
Stratégie 2 : p = 43,3 %
Stratégie 3 : p = 35 %
Stratégie 4 : p = 20 %
Bref, la meilleure stratégie consiste ici à laisser passer les deux premiers candidats.
Mais pour les valeurs plus grande ? Il existe forcément une stratégie meilleure que les autres, mais laquelle ? Et la solution est plutôt simple : même si vous devez auditionner 100 000 secrétaires, il existe toujours une stratégie permettant de trouver le meilleur avec une probabilité supérieure à 36% ! Cette stratégie, c'est la stratégie n/e : il faut laisser passer le premier tiers (36.79% des candidats, pour être un peu plus précis) des candidats, puis prendre le premier des candidats meilleurs. Et on va le prouver !
Le jeu du gogolLe problème des secrétaires trouve ses origines dans la rubrique Mathematical Games de Martin Gardner dans le numéro de février 1960 du Scientific American. Le problème y est présenté sous la forme du "jeu du gogol" : un joueur écrit sur des feuilles des nombres quelconques, arbitrairement grands ou petits (d'où le nom du jeu : on peut y écrire des nombres aussi grand qu'un gogol, ie, 10100), le but étant pour l'autre joueur de les retourner successivement, mais de s'arrêter sur le plus grand d'entre eux. La question de la stratégie optimale à suivre pour le deuxième joueur revient à résoudre le problème des secrétaires. La solution arrivera dans la même rubrique du magazine, le mois suivant. On retrouvera plus tard le même problème sous le nom de "problème du mariage" (un Don Juan fait défiler des candidate pour son mariage, jusqu'à faire un choix), ou sous d'autres appellations tout aussi sexistes (problème de la dot, problème du concours de beauté, ...).
Les origines du problème semble cependant remonter au XVIIe siècle, après que l'astronome allemand Johannes Kepler a perdu sa première femme à cause du choléra. Bien décidé à en trouver une nouvelle, il a cherché à ne pas faire la même erreur que pour son premier mariage, qui lui avait été arrangé. Pour ce faire, il a consacré deux ans de sa vie à chercher la femme idéale, et 11 ont répondu à l'appel. De nombreuses lettres de Kepler relatent son processus de décision pas tout à fait au point. Le problème se termine bien : il finira par choisir la cinquième, ils se marièrent et eurent beaucoup (7) d'enfants.
En fait, Kepler n'a pas réellement inventé le problème des secrétaires (la plupart des hypothèses du problème ne sont pas respectées, puisqu'il s'est autorisé à revenir sur ses choix), mais il a quand même énoncé le premier problème d'arrêt optimal, en inventant au passage le principe du speed-dating (qui dure deux ans).
En fait, Kepler n'a pas réellement inventé le problème des secrétaires (la plupart des hypothèses du problème ne sont pas respectées, puisqu'il s'est autorisé à revenir sur ses choix), mais il a quand même énoncé le premier problème d'arrêt optimal, en inventant au passage le principe du speed-dating (qui dure deux ans).
Cas général
Revenons au problème général, avec n secrétaires. Les informations que l'on a à notre disposition limitent pas mal les différentes stratégies possibles. En fait, les seules stratégies envisageables sont les stratégie k (k ∈ [0 ; n-1]) : on interroge les k premiers candidats pour se donner une idée de leur niveau en les rejetant systématiquement, puis, parmi les n-k candidats suivants, on choisit le premier à être meilleur que les k premiers. Reste à savoir quelle est, en fonction de n, la valeur de k idéale.
Revenons au problème général, avec n secrétaires. Les informations que l'on a à notre disposition limitent pas mal les différentes stratégies possibles. En fait, les seules stratégies envisageables sont les stratégie k (k ∈ [0 ; n-1]) : on interroge les k premiers candidats pour se donner une idée de leur niveau en les rejetant systématiquement, puis, parmi les n-k candidats suivants, on choisit le premier à être meilleur que les k premiers. Reste à savoir quelle est, en fonction de n, la valeur de k idéale.
Notons j la position de ce mystérieux candidat meilleur que les autres. La probabilité que j soit une valeur fixée à l'avance est de 1/n.
Si j ≤ k, alors le candidat n°j sera ignoré, et donc, non choisi.
Si j = k+1, c'est que le meilleur candidat arrive pile au bon moment : il est choisi.
Si j ≥ k+2, le candidat n°j sera sélectionné seulement s'il n'y a pas de candidat opportuniste (meilleur que les k premiers) entre la position k+1 et j-1. Ceci n'arrivera qu'avec une probabilité de k/(j-1) : la probabilité que le meilleur des (j-1) premiers soit dans les k premiers (formellement, c'est la probabilité de choisir le j-ième candidat sachant que c'est le meilleur).
Si j ≤ k, alors le candidat n°j sera ignoré, et donc, non choisi.
Si j = k+1, c'est que le meilleur candidat arrive pile au bon moment : il est choisi.
Si j ≥ k+2, le candidat n°j sera sélectionné seulement s'il n'y a pas de candidat opportuniste (meilleur que les k premiers) entre la position k+1 et j-1. Ceci n'arrivera qu'avec une probabilité de k/(j-1) : la probabilité que le meilleur des (j-1) premiers soit dans les k premiers (formellement, c'est la probabilité de choisir le j-ième candidat sachant que c'est le meilleur).
La probabilité que la stratégie k permette de trouver le meilleur candidat est donc :

En simplifiant :
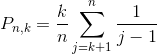
Pour des petites valeurs de n, on peut calculer ces probabilités pour toutes les valeurs de k afin de déterminer la stratégie optimale :
Pour n = 3, P est maximal pour k = 1 (P = 0.5)
Pour n = 4, P est maximal pour k = 1 (P = 0.458)
Pour n = 5, P est maximal pour k = 2 (P = 0.433)
Pour n = 6, P est maximal pour k = 2 (P = 0.428)
Pour n = 7, P est maximal pour k = 2 (P = 0.414)
Pour n = 8, P est maximal pour k = 3 (P = 0.410)
Pour n = 9, P est maximal pour k = 3 (P = 0.406)
Pour n = 10, P est maximal pour k = 3 (P = 0.398)En poursuivant les calculs, on peut se convaincre que n/k tend vers e.
Pour n = 4, P est maximal pour k = 1 (P = 0.458)
Pour n = 5, P est maximal pour k = 2 (P = 0.433)
Pour n = 6, P est maximal pour k = 2 (P = 0.428)
Pour n = 7, P est maximal pour k = 2 (P = 0.414)
Pour n = 8, P est maximal pour k = 3 (P = 0.410)
Pour n = 9, P est maximal pour k = 3 (P = 0.406)
Pour n = 10, P est maximal pour k = 3 (P = 0.398)En poursuivant les calculs, on peut se convaincre que n/k tend vers e.
Pour des valeurs de n plus élevées, on va plutôt déterminer une valeur approchée de Pn,k. Un peu de calcul intégral permet de voir que
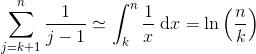
La probabilité de succès de la stratégie k est donc environ égale à Pn,k = (k/n) ln(n/k). Il n'y a plus qu'à chercher pour quelle valeur de k cette probabilité est maximale.
Posons x = (k/n). La fonction f(x) = x ln(1/x) est maximale (si si, je vous l'assure) lorsque x = 1/e ≈ 0.368, ce qui signifie que la probabilité est maximale quand le rapport entre k et n vaut approximativement 36.8 %.
La meilleure stratégie, pour un nombre de candidat n, est donc la stratégie n/e. Cette stratégie offre une probabilité de succès valant f(1/e) = 1/e ≈ 0.368.
Posons x = (k/n). La fonction f(x) = x ln(1/x) est maximale (si si, je vous l'assure) lorsque x = 1/e ≈ 0.368, ce qui signifie que la probabilité est maximale quand le rapport entre k et n vaut approximativement 36.8 %.
La meilleure stratégie, pour un nombre de candidat n, est donc la stratégie n/e. Cette stratégie offre une probabilité de succès valant f(1/e) = 1/e ≈ 0.368.
Il y a des tas d'autres problèmes d'arrêt optimal, comme celui du jeu d'Arthur "à prendre ou à laisser". Puisqu'il paraît que le jeu revient à la télé à la rentrée, ça me fera une bonne excuse pour faire d'autres articles sur le
L’aléa joue un rôle déterminant dans des contextes variés et il est souvent nécessaire de le prendre en compte dans de multiples aspects des sciences de l’ingénieur, citons notamment les télécommunications, la reconnaissance de formes ou l’administration des réseaux. Plus généralement, l’aléa intervient aussi en économie (gestion du risque), en médecine (propagation d’une épidémie), en biologie (évolution d’une population) ou en physique statistique (théorie des transitions de phases). Dans les applications, les données observées au cours du temps sont souvent modélisées par des variables aléatoires corrélées dont on aimerait prédire le comportement. L’objet de ce cours est de formaliser ces notions en étudiant deux types de processus aléatoires fondamentaux en théorie des probabilités : les chaînes de Markov et les martingales. Des applications variées seront présentées pour illustrer ces concepts.
Ce cours introduit les notions de base de la théorie des probabilités, c'est-à-dire l'analyse mathématique de phénomènes dans lesquels le hasard intervient. Il insistera en particulier sur les deux notions majeures qui sont les fondements de cette théorie : le conditionnement et la loi des grands nombres. L'enseignement a pour objectif l'acquisition du raisonnement probabiliste et l'apprentissage de la modélisation probabiliste et de la simulation. Cette modélisation est fondamentale dans de nombreux domaines d'applications. Le cours est illustré par des exemples et des expérimentations numériques. Il introduit aussi quelques notions de la théorie de la mesure (qui est le fondement axiomatique de la théorie des probabilités) et il offre une ouverture vers la statistique. Pendant cet enseignement, les élèves réaliseront un projet de simulation en binôme qui sera pris en compte pour la note du module.
Référence bibliographique :"Promenade aléatoire: chaînes de Markhov et martingales", Thierry Bodineau (2013)
_____________________________________
- Toutes les solutions proposées à base de 90x(0,5)^10 ou 91x(0,5)^10 sont évidemment fausses. Cela voudrait dire qu'au bout de 1035 tirages par exemple on a une probabilité supérieure à 1 d'avoir 10 "faces" consécutifs. La probabilité va tendre vers 1 sans jamais l'atteindre car bien évidemment il ne sera jamais certain, même au bout d'un millions de fois, d'avoir la certitude parfaite à 1 d'avoir 10 "faces" de suite à un moment ou un autre.J'avais répondu un peu vite dans un premier temps, en combinant des probabilités en (1023/1024) entre eux. Je revois mon raisonnement car mon dénombrement comptait "double" certaines séquences particulières. Voici le nouveau raisonnement, bien plus fiable même si un peu lourd. A ce sujet, voici quelques liens qui traitent de ce sujet et permettent aussi de valider les résultats :-> permet de lancer par exemple 1000 fois 100 lancers de dés et fournit le pourcentage de au moins 10 coups identiques successifs-> résultat fourni pour 10 successifs dans 100 tirages = 0,09 au centième près (9% à l'unité près)Reprenons pour le raisonnement, qui est en fait un dénombrement complet des différents cas par récurrence :Notons Un le nombre de suites de n lancers de pile ou face, ne contenant AUCUNE séquence de 10 tirages consécutifs égaux (que ce soit des PILE ou FACE).On peut séparer cette suite Un en 9 types différents de suites, en considérant les derniers termes de cette suite, dénombrés ainsi :(1) si les 2 derniers termes de la suite sont différents, il s'agit de PF ou FP.----- Si la suite finit par FACE, donc les (n-1) premiers termes sont des suites U(n-1) se finissant par PILE.----- Si la suite finit par PILE, donc les (n-1) premiers termes sont des suites U(n-1) se finissant par FACE.-- La somme de ces 2 types de suites (U(n-1) se finissant par PILE et U(n-1) se finissant par FACE) sont bien évidemment TOUTES les suites U(n-1). Il y a donc U(n-1) suites de type (1)(2) si les 2 derniers termes de la suite sont identiques et le terme d'avant différent, il s'agit de PFF ou FPP.----- Si la suite finit par FF, donc les (n-2) premiers termes sont des suites U(n-2) se finissant par PILE.----- Si la suite finit par PP, donc les (n-2) premiers termes sont des suites U(n-2) se finissant par FACE.-- La somme de ces 2 types de suites (U(n-2) se finissant par PILE et U(n-2) se finissant par FACE) sont bien évidemment TOUTES les suites U(n-2). Il y a donc U(n-2) suites de type (2)(3) si les 3 derniers termes de la suite sont identiques et le terme d'avant différent, il s'agit de PFFF ou FPPP.----- Si la suite finit par FFF, donc les (n-3) premiers termes sont des suites U(n-3) se finissant par PILE.----- Si la suite finit par PPP, donc les (n-3) premiers termes sont des suites U(n-3) se finissant par FACE.-- La somme de ces 2 types de suites (U(n-3) se finissant par PILE et U(n-3) se finissant par FACE) sont bien évidemment TOUTES les suites U(n-3). Il y a donc U(n-3) suites de type (3)...(9) si les 9 derniers termes de la suite sont identiques et le terme d'avant différent, il s'agit de PFFFFFFFFF ou FPPPPPPPPP.----- Si la suite finit par FFFFFFFFF, donc les (n-9) premiers termes sont des suites U(n-9) se finissant par PILE.----- Si la suite finit par PPPPPPPPP, donc les (n-9) premiers termes sont des suites U(n-9) se finissant par FACE.-- La somme de ces 2 types de suites (U(n-9) se finissant par PILE et U(n-9) se finissant par FACE) sont bien évidemment TOUTES les suites U(n-9). Il y a donc U(n-9) suites de type (9)Il n'y a aucun recouvrement entre ces 9 types de suites (elle sont différentes entre elles) et il n'y a pas d'autres types de suites possibles pour une suite Un (on couvre tous les cas possibles de Un).On a donc, pour n>9 :Un = U(n-1) + U(n-2) + U(n-3) + U(n-4) + U(n-5) + U(n-6) + U(n-7) + U(n-8) + U(n-9)La probabilité cherchée est donc U100/(2^100). Pour définir U100, il suffit de déterminer "à la main" les 9 premières suites et ensuite de calculer de proche en proche les Un suivants par récurrence.U1 = 2 (toutes les suites de 1 tirage sont différentes de la suite 10 tirages consécutifs égaux)U2 = 4 (toutes les suites de 2 tirages sont différentes de la suite 10 tirages consécutifs égaux)U3 = 8 (toutes les suites de 3 tirages sont différentes de la suite 10 tirages consécutifs égaux)...U9 = 2^9 = 512 (toutes les suites de 9 tirages sont différentes de la suite 10 tirages consécutifs égaux)U10 = 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2U10 = 1022ce qui correspond à la réalité car U10 correspond à toutes les suites de 10 tirages (1024) sauf les suites FFFFFFFFFF et PPPPPPPPPP. Donc 1022.U11 = 1022 + 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4U11 = 2042ce qui correspond à la réalité car U11 correspond à toutes les suites de 11 tirages (2048) sauf les suites FFFFFFFFFFF, FFFFFFFFFFP, PPPPPPPPPPF, PPPPPPPPPPP, PFFFFFFFFFF et FPPPPPPPPPP. Donc 2048-6 = 2042.On peut procéder au calcul de U100 de proche en proche, par exemple en faisant une bête feuille de calcul Excel.On tombe sur U100 = 1157797210644820000000000000000 suites différentes avec AUCUNE séquence de 10 tirages consécutifs égaux.D'où U100 / 2^100 = 0,91334095565163475936636435849895...est la probabilité de n'avoir AUCUNE séquence de 10 consécutifs égaux (qu'il s'agisse de PILE ou FACE)donc la probabilité d'avoir au moins 10 consécutifs égaux (de PILE OU FACE) est de1 - U100/2^100 = 0,086659044348365240633635641501046...Donc la probabilité d'avoir au moins 10 FACES consécutifs est la même probabilité que d'avoir au moins 10 PILES consécutifs et représente la moitié exactement de cette probabilité, soit :0,043329522174182620316817820750523...@GloumePour revenir sur la suite Un, elle donne le nombre des différents n tirages qui ont comme caractéristique de n'avoir pas 10 éléments ou plus consécutifs égaux (pas 10 FACE ni 10 PILE).Pour reprendre peut-être plus simplement sur le principe du découpage de Un, si une suite de n tirages se termine par 2 éléments différents (cas (1) du découpage en 9 cas), alors cette suite de n tirages ne comprend pas 10 éléments consécutifs égaux si et seulement si les (n-1) premiers éléments de ce tirage ne comprennent pas eux-mêmes 10 éléments consécutifs égaux.Pour reprendre le cas (3), si une suite de n tirages se termine par 3 éléments égaux le (n-4) étant différent (cas PFFF ou FPPP), alors cette suite de n tirages ne comprend pas 10 éléments consécutifs égaux si et seulement si les (n-4) premiers éléments de ce tirage ne comprennent pas eux-mêmes 10 éléments consécutifs égaux.Ainsi de suite, on s'aperçoit que les suites de cas (1) (=U(n-1)), de cas (2) (=U(n-2)), ..., de cas (9) (=U(n-9)) sont tous distincts (pas de recouvrement entre ces cas) et forment à eux 9 l'ensemble de tous les tirages de taille n possibles sans 10 éléments consécutifs égaux (=Un).Donc Un = U(n-1) + U(n-2) + U(n-3) + U(n-4) + U(n-5) + U(n-6) + U(n-7) + U(n-8) + U(n-9)
 Connectez-vous pour commenter des réponses
Connectez-vous pour commenter des réponses











































Ce magazine essayant de trouver le moyen de renforcer ses chances de gagner au loto (Doux rêve), s'était penché sur une constatation statistique sur la sortie des différents tirages, ce qui se rapproche de vos tirages de dés...
A regarder les tirages , on s'aperçoit qu'un tirage (12345) au loto n'est toujours pas sorti depuis la création de la Française des Jeux, pourtant on sait très bien qu'il a autant de chances de sorties (29,5,13,43,41) qui par exemple est déjà sorti deux fois !
Le premier même si il a autant de chances de sortie nous parait totalement farfelu, et le second ne nous étonne guère...Notre fameuse mauvaise interprétation du hasard...
Mais pour renforcer ses chances lorsque l'on joue, cette étude nommée "Le poids de la grille" préconisait de jouer des grilles qui s'approchaient de la moyenne des sommes de tous les numéros d'une grille !!!
Je m'explique, en arrondissant a 50 le nombre de numéros, la moyenne de 50 étant 25, on multipliait 25X5 ce qui faisait 125 que l'on considérait comme une moyenne de poids d'une grille de sortie...
En jouant de cette manière, on tombait il me semble à 70% de chances de faire partie d'un tirage gagnant, si notre sélection de numéros avoisinait la somme de 125 à plus ou moins 10% près ( 115,125)
Etrange manière de jouer, mais peut être pas si stupide...